Interpolation of Rainfall in Switzerland using a Regularized Spline with Tension

William W. Hargrove
Geographic Information and Spatial Technologies Group
Oak Ridge National Laboratory
P.O. Box 2008, M.S. 6274
Oak Ridge, TN 37831-6274
hnw@fire.esd.ornl.gov

Abstract

Given rainfall measured at 100 stations across Switzerland, and a digital elevation model, rainfall at an additional 367 stations was estimated two ways using a regularized spline with tension and smoothing. One set of estimates resulted from simple planar interpolation of rainfall measurements without regard to elevation. Another estimate was produced by volumetric interpolation of rainfall with elevation, followed by intersecting the elevation model with the interpolated volume.

Both spline techniques performed similarly, and provided accurate estimates of mean and median rainfall. While neither spline method predicted the absolute values of extreme rainfall well, both adequately predicted the spatial pattern of high and low rainfall. Thus, the locations of highest and lowest rainfall were properly identified, although the range of true rainfall values were not accurately reproduced by the splined estimates.

Keywords: interpolation, rainfall, SIC97, spline, Switzerland

Introduction

The regularized spline with tension and smoothing is a radial basis function which can be used to interpolate surfaces from data collected at scattered points (Talmi and Gilat 1977, Wahba 1990, Mitasova and Mitas 1993, Mitasova and Hofierka 1993). The implementation used here was originally written by Helena Mitasova, and adapted for the Geographic Resources Analysis Support System (GRASS) GIS system (Mitasova 1992a, Mitasova 1992b, Mitasova et al., 1995). The GRASS implementation employs an advanced quadtree regional segmentation procedure which can efficiently divide and process large extents at high resolution which contain large numbers of observations. For additional information on the GRASS spline interpolator, see http://www.cecer.army.mil/grass/viz/interp.html.

Important spline parameters are of two general types: those that control the size and connectivity of the individually-interpolated regional segments, and those that control the character of the interpolated surface itself. Of the former, segmax controls the maximum number of points per segment of the region, and effectively establishes the size of individual portions of the map which will be individually interpolated. Areas densly populated with data will be divided into more, smaller segments than areas with few data points. The npmin parameter establishes how many points are to be considered outside the current segment. A high setting of npmin ensures a smooth and seamless interconnection between segments.

The tension parameter is perhaps the most important with regard to the nature of the final interpolated surface. High tension settings cause the surface to remain at trend, while low tension permits the surface to overshoot data points. Conceptually, if the surface were a rubber sheet or membrane, the tension parameter can be thought of as changing the flexibility of the membrane from thin and stretchy to thick and stiff. A related parameter, smoothing, establishes how close the surface must come to each data point; a smoothing of zero insists that the surface pass exactly through the observation, but the surface may wrinkle or distort unnaturally in order to do so. The smoothing parameter can also be used to reflect the level of confidence or measurement error in the observed data.

Two Strategies for Interpolating Rainfall in Switzerland

Two distinct rationales were used to estimate rainfall in Switzerland using the regularized spline with tension. The first method was to simply interpolate the raingauge values, without regard to elevation. Because rainfall data were provided at only 100 points across a 75 thousand square kilometer area, and because the relationship between elevation and rainfall is not constant, but changes, for example, from windward to leeward slopes, it was initially deemed that the reslution of the observations did not merit a finely-tuned interpolation approach.

Nevertheless, the second interpolation method was considerably more sophisticated, and considered elevation data as well as observed rainfall. A volume was defined whose bottom and top were established by the lowest and highest elevations among the points to be predicted. This volume was populated with the 100 observations, and the regularized spline was used in three dimensions to volumetrically interpolate rainfall everywhere within this volume. Thus, the elevation information as well as the x,y geographic locations were taken into account by the interpolator. Finally, the digital elevation model (DEM) was intersected with this volume, and the points to be predicted were dropped onto the plane projection of this intersection.

Parameter Settings

For both interpolations, a geographic region of 341 columns by 220 rows with a horizontal resolution of 1 km was established. Such fine resolution may not have been warranted by the sparse nature of the data, but the observed rainfall data exhibited high-gradient amplitude changes over fine spatial scales, and this resolution was achievable with little computational cost.

For the two-dimensional interpolation, tension was set to 130, with a smoothing of 0.2mm. Because only 100 data points were supplied, segmentation of the region was not necessary. Thus, a segmax of 400 was used, and npmin of 100, and the entire map was interpolated in a single pass.

For the three-dimensional volumetric interpolation, the z range of the points to be estimated was from 193 to 3021m, while the supplied points were all between 236 to 2418m. Thus, the bottom of the volume was set at 150m, and the top at 3150m, with 10 z levels of 300m resolution in-between. Because the z range of points to be predicted was outside the range of the observed points, overshoots in the data were essentially required. Therefore, the tension parameter was lowered to 5, with a smoothing of 0.05mm. The segmentation parameters were the same as previously used.

Interpolation Results

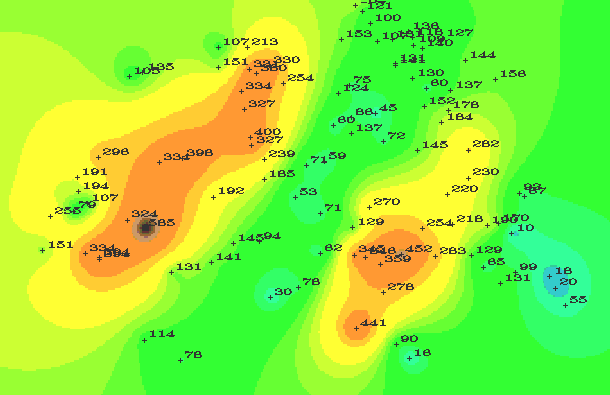
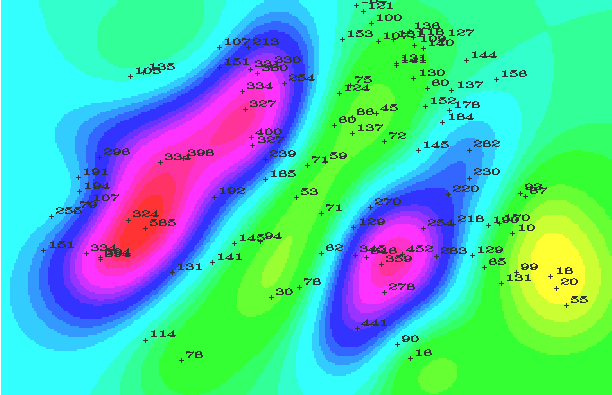
Rainfall surfaces resulting from the 2D and 3D spline interpolations, with observed rainfall values overlain, are shown in Figures 1a and b, respectively. Both surfaces seem responsive to changes in the magnitude of the observations.

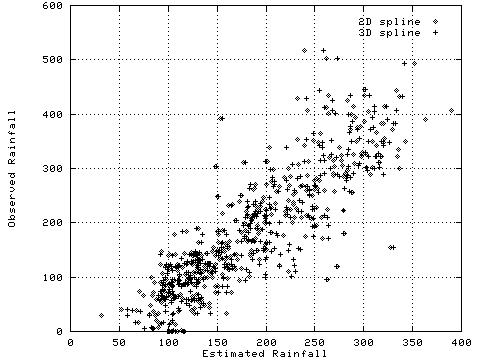
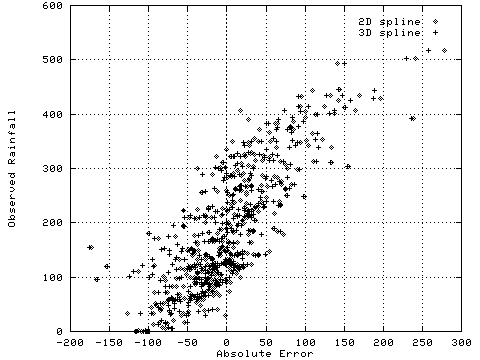
The 2D and 3D results were very similar. A scatterplot of observed vs. estimated rainfall (Figure 2) shows that both techniques did a reasonable job of estimating rainfall, and that neither method was greatly superior. Errors increase slightly with magnitude. Comparison of a line fitted to the error points with the observed=expected line indicate a slight tendency to overestimate low rainfall or dew values, and a slight tendency to underestimate large rainfall events.

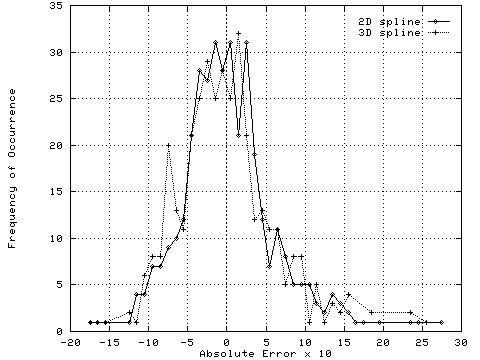
The statistical distribution of absolute errors (Figure 3a) is reasonably symmetrical about zero, the histogram slightly shifted toward overestimation. The histogram of percent error (Figure 3b) is also centered on zero, but is slightly skewed toward underestimation in terms of percent error.

Comparison of sample statistics among the observed rainfall, the 2D spline estimates, and the 3D spline estimates (Table 1) indicates a reasonable match between both interpolated rainfall estimates and the true values in terms of mean and median. However, both splined rainfall estimates had much narrower ranges and much lower variance than the true values. The 2D spline had a greater maximum, while the 3D had a smaller minimum, but both extremes were much narrower than the range of true rainfall values.

In fact, the estimates for the 10 lowest rainfall observations were all low for both splines, while the estimates for the 10 highest rainfall observations were all high for both. Four and five of the 10 largest absolute errors in the 2D and 3D spline estimates were among these 10 highest or lowest rainfall sites.

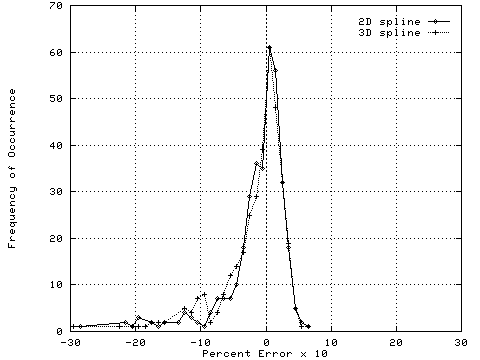
Figures 4a and b show the spatial dispersion of absolute errors (observed-predicted) for the 2D and 3D interpolations. The spatial arrangement of errors is highly nonrandom; both undershoots and overshoots are strongly correlated spatially. Of the 10 locations receiving greatest rainfall, the 2D spline shared 3 and the 3D estimates shared 2. Of the 10 driest sites, the 2D spline shared none; the 3D estimates shared 2. There was a strong correlation between magnitude of absolute error and observed rainfall for both sets of estimates (Figure 5).

Discussion

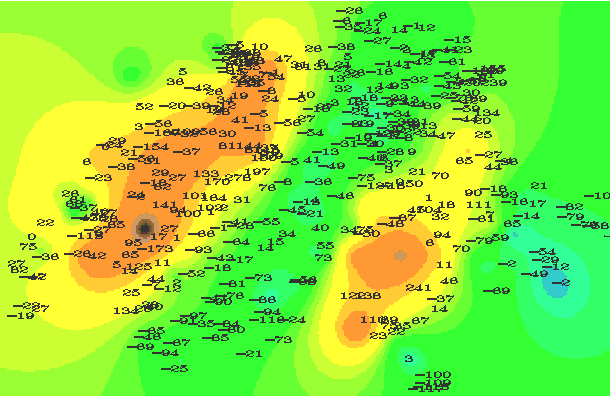
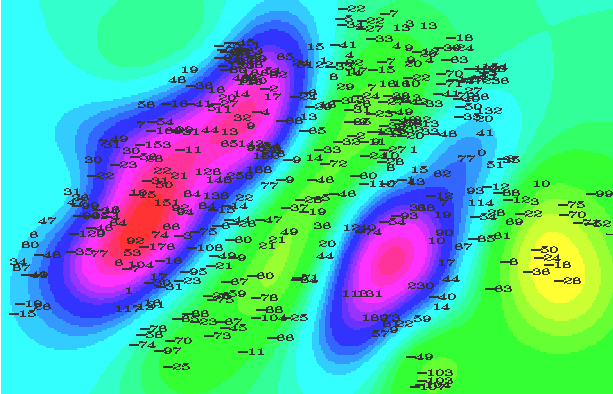
Although mean rainfall was well-represented, the spline interpolator did a relatively poor job of predicting the absolute values of rainfall extrema. This results from the conservative tendency of the spline, in the absence of data, to return to trend. Where the splined surface is low, it should have been lower; where the splined surface is high, it should have been higher.

However, this strong spatial autocorrelation among undershoots and overshoots is indicative that the spatial pattern of changes in rainfall was well-represented by the splined surface. Lowest values were generally to be found at the lowest parts of the surface, and vice versa. Both of the spline interpolations adequately captured the relative spatial trends in rainfall.

The regularized spline with tension has other characteristics which are desirable for rainfall or fallout estimation. In contrast with kriging, spatial stationarity across the map is not assumed. The relationship between rainfall and elevation is not stationary, but depends on the prevailing wind direction and incoming moisture loads (Daly et al. 1994). Even co-kriging with elevation will be a poor choice for interpolating such a statistically variable phenomenon. With a spline, however, fitting functions go to higher mathematical orders as necessary to fit observed data within the current segment, changing to adapt to local statistical conditions. Furthermore, no pre-modeling is necessary; fast, nearly automatic interpolation of rainfall or contamination using splines would be possible within a Decision Support System (DSS) under emergency conditions. Indeed, the spline is not limited to any single semivariogram rainfall model.

The more elaborate 3D spline approach proved no more accurate than the simpler 2D strategy. It is suspected that the 3D technique would have proven more accurate than the 2D technique with a higher density or count of known rainfall observations over a broader range of locations and elevations.

Conclusions

The regularized spline with tension provided a simple, rapid interpolation and characterization of rainfall (and, ostensibly, fallout) across Switzerland, given sparse observations. The fact that no explicit statistical modeling is necessary, and that the spline can model non-stationary relationships makes it amenable to automation within an emergency DSS.

In the absence of data (i.e., when data observations are sparse), the spline interpolator tends toward trend. This conservative characteristic may be desirable under certain circumstances. Where the primary interest is in the spatial pattern (i.e., where to find the highest or lowest fallout levels), or in calculating mean or median dosages over larger areas, the spline interpolator would represent an excellent choice. Interpolation by spline may not be a good choice when it is desired to calculate peak contaminant dosages or mean rainfall/radiation levels over small "hot-spots."

Acknowledgements

The author acknowledges the support of the Integrated Modeling Project, funded by the U.S.D.A. Forest Service Southern Global Change Program. Helena Mitasova suggested methodology for the 3D spline approach. Jaro Hofierka supplied executable binary code for the LINUX operating system.

References

Daly, C., Neilson, R., and Phillips, D. (1994) A statistical-topographic model for mapping climatological precipitation. J. Applied Meteorology, 33,140-158.

Mitasova, H. and Mitas, L. (1993) Interpolation by Regularized Spline with Tension: I. Theory and Implementation, Mathematical Geology, 25, 641-655.

Mitasova, H. and Hofierka, L. (1993) Interpolation by Regularized Spline with Tension: II. Application to Terrain Modeling and Surface Geometry Analysis, Mathematical Geology, 25, 657-669.

Mitasova, H. (1992a) New capabilities for interpolation and topographic analysis in GRASS, GRASSclippings, v.6, No. 2 (summer), p.13.

Mitasova, H. (1992b) Surfaces and modeling, GRASSclippings, v.6, No. 3 (winter), p.16-18.

Mitasova, H., Mitas, L., Brown, W.M., Gerdes, D.P., Kosinovsky, I., and Baker, T. (1995) Modeling spatially and temporally distributed phenomena: new methods and tools for GRASS GIS. International Journal of Geographical Information Systems (London: Taylor & Francis), vol. 9, No. 4, p.433-446.

Talmi, A. and Gilat, G. (1977) Method for Smooth Approximation of Data, Journal of Computational Physics, 23, p.93-123.

Wahba, G., (1990) Spline Models for Observational Data, CNMS-NSF Regional Conference series in applied mathematics, 59, SIAM, Philadelphia, Pennsylvania.